导读：这是一篇相对专业的探讨内算与外算的文章，因此写的略长，尽量避开太过专业的名词，有兴趣的可以继续观看。

上次，我们讲到南宋数学家秦九韶的《数术九章》是中国古代数学史上的一座丰碑。

与纯粹探讨理论的著作不同，

这本书从诞生之初就带有强烈的现实主义色彩。

秦九韶本人曾为官多年，

深知国家运转中的种种弊病：

从历法失准到赋役不均，从工程浪费到军需混乱。

在他看来，这一切乱象的根源，

很大程度上在于管理者缺乏“数术”知识，

无法进行精确的计算和理性的规划。

因此，他将《数术九章》全书分为九大类，

每一类都直面一个具体的社会经济问题。

而在每一章的开篇，他都精心撰写了一首序诗。

这些诗歌，并非简单的点缀，而是全书的“魂”。

它们的作用在于：

将具体的数学问题，

提升到“道”、“天时”、“仁政”的哲学高度，

阐明数学是探究宇宙规律、辅佐国家治理的根本工具。

同时，毫不客气地指出当时官吏的无能与欺诈，

强调精准计算对于实现社会公平、杜绝腐败的重要性。

当然，字里行间中，他也展现了中国本土数学方法的精妙与源远流长，

建立一种基于理性与科学的文化自信。

（实际上，据我从众多古籍中搜集的证据了解，

同时期的西方并没有数学，一直到宋末元初时期，

蒙古人掠夺了很多汉人工匠随军西征时，

才带一些东西到西方。）

回到数术九章，

可以说，这九首诗为冰冷的数学注入了炽热的人文关怀与政治抱负。

读懂了它们，才能真正理解秦九韶写下这部巨著的最终目标：

以数学为利器，匡时济世。

下面讲讲这九首诗中的第一首。

述大衍第一

昆仑磅礴，道本虚一。圣有大衍，微寓于易。

奇余取策，群数皆捐。衍而究之，探隐知原。

数术之传，以实为体。其书九章，惟兹弗纪。

历家虽用，用而不知。小试经世，姑推所为。

宇宙如昆仑山般磅礴，

而其本源的“道”是虚静而归于“一”的。

古代圣人创立了“大衍之术”，

其精深的道理蕴含在《易经》之中。

（大衍术）通过取不同的余数（奇余）来推算，

可以抛开那些庞杂的（无法直接处理的）数字。

推演并深入研究它，

就能探究幽隐的奥秘，

知晓事物的本原。

自古流传下来的数学著作（如《九章算术》），

都以解决实际问题为核心。

但《九章算术》里，却没有记载这种（大衍）算法。

如今的历法家们虽然也在使用这类方法，

但很多人只是机械套用，并不理解其根本原理。

我在此小试牛刀，

将它应用于经世济民的实际问题中，

姑且推演一番它的作用。

这首诗提出了全书最核心、最耀眼的数学成就，

大衍总数术（现代称为“中国剩余定理”）。

这也是秦九韶颇为自豪的一件事。

秦九韶将他的算法与宇宙探源的哲学思想联系起来。

大衍术正是从一堆看似无关的“余数”中，

反推出那个唯一的“本原数”。

这既是数学求解，也是哲学溯源。

大衍术的技术核心是指“奇余取策，群数皆捐”。

面对一个巨大而未知的总数，我们不需要知道它本身，

只需要知道它被不同数除所得到的“余数”，

就能反推出这个总数。

这是极其高明的化繁为简思想。

当然，秦九韶在诗里写道：

“历家虽用，用而不知”，

直接批评了当时的从业者缺乏理论深度，

只会依样画葫芦。

同时，通过“《九章》弗纪”点明这是对传统数学的重大补充和发展，

展现了强烈的创新自信。

这一章主要解决的是复杂的历法计算、兵员点卯、财物计数等问题。

也就是大衍术的应用。

那么今天我用最通俗的语言来讲讲这个大衍术，

并理清楚其与易经的关系。

有句话叫“韩信点兵，多多益善。”

为什么呢？

因为韩信掌握了点兵的算法，

通过士兵报数立马可以推算出当前有多少人。

那么他是怎么做到的？

今天来解密下，这是和秦九韶的大衍求一术密切相关的问题。

想象一下，你就是韩信，在清点士兵，

但人数太多，懒得一个个细数。

于是你命令他们：

“3人一排，最后剩下2人！”

“5人一排，最后剩下3人！”

“7人一排，最后剩下2人！”

问题来了：至少有多少名士兵？

这个问题出自南北朝的数学著作《孙子算经》，

原文是“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”

“大衍术”（中国剩余定理）就是为了完美解决这类问题而生的。

它的核心目标是：根据一个数被不同除数除所得到的余数，反推出这个数本身。

那么如何通过大衍术来“解题”呢？

《孙子算经》里有一段像诗歌一样的解法口诀：

“三人同行七十稀，五树梅花廿一支，

七子团圆正半月，除百零五便得知。”

我们把它翻译成现代的解题步骤，

来解决上面的将军点兵问题。

第一步：找到三个“神奇的数字”

这个算法最巧妙的地方，

是先找到三个“对别人没影响，只对自己有用的”数字。

针对“除以3”：

我们要找一个数，它必须是5和7的公倍数（这样除以5和7都余0，对它们没影响），

同时，这个数除以3要余1。

5×7 = 35。但35÷3 = 11...余2，不行。

35的倍数里找：35×2 = 70。70÷3 = 23...余1。找到了！

这就是口诀里的“三人同行七十稀”。

针对“除以5”：

找一个数，它必须是3和7的公倍数，同时除以5要余1。

3×7 = 21。21÷5 = 4...余1。

一次就找到了！这就是“五树梅花廿一支”。

针对“除以7”：

找一个数，它必须是3和5的公倍数，同时除以7要余1。

3×5 = 15。15÷7 = 2...余1。

也找到了！这就是“七子团圆正半月”（半月即15天）。

我们现在有了三个“神奇数字”：70，21，15。

第二步：合体！

现在，把题目中给出的“余数”和我们找到的“神奇数字”乘起来，再相加。

（除以3的余数2）×（它的神奇数字70）= 140

（除以5的余数3）×（它的神奇数字21）= 63

（除以7的余数2）×（它的神奇数字15）= 30

把它们加起来：140 + 63 + 30 = 233。

第三步：做最后的“微调”

这个233已经满足了所有余数条件，

但可能不是最小的那个。

我们需要找到3、5、7的最小公倍数。

3×5×7 = 105。（这就是口诀里的“除百零五便得知”）

用233不断减去105，直到得到一个最小的正整数：

答案揭晓：至少有23名士兵。可以验证一下：

23÷3 = 7...余2

23÷5 = 4...余3

23÷7 = 3...余2

完美符合！

因为这里不是专门的数学研讨，所以就不给出完整的证明，

我们来说说它和易经有什么关系。

最早的易经起卦，

不是用铜钱或者数字直接起，

而是用蓍草来起，

起法也叫“大衍术”。

具体过程如下：

《易经·系辞传》里有句总纲：

“大衍之数五十，其用四十有九。”

目标：我们要通过一个“游戏”，来得出六个数字中的一个（6, 7, 8,或9），这个数字代表卦象中的“一爻”。重复这个游戏六次，就能得到完整的六爻卦象。

游戏开始（求第一爻）：

准备阶段：天地之始

拿出你的50根“蓍草”。

先抽出一根放在旁边，永远不用。

这代表“太极”，是宇宙的本源，

它不动，只是静静地看着一切发生。

所以，我们实际用来计算的，是剩下的49根。

这就是“其用四十有九”。

第一步：一分为二（象征阴阳）

闭上眼睛，心无杂念，将这49根牙签随机分成左右两堆。

第二步：天、地、人三才

从右手边的那堆里，拿出一根，夹在你的左手小指和无名指之间。这根象征着“人”，位于天地之间。

第三步：以四计数（象征四季轮转）

现在，开始处理左手边那堆。以4根为一组，不断地数，看看最后剩下几根（可能剩1、2、3根，如果正好数完，就是剩下4根）。

把这些剩下的（1-4根）也夹在你的左手指缝里（比如无名指和中指间）。

接着，处理右手边剩下那堆，同样以4根为一组地数，把最后剩下的（1-4根）也夹在左手指缝里（比如中指和食指间）。

得出第一次结果（一变）

现在，你手上夹着三小撮牙签：最初从右边拿的1根，左边剩下的，右边剩下的。

把这三小撮合在一起，数一下总数。你会惊奇地发现，这个数字必定是5或者9。

把这一小堆（5或9根）放到旁边，把桌上那些被4整除的大部队收拢起来。桌上现在应该剩下44根（49-5）或40根（49-9）。

重复与演进（二变与三变）

“二变”：把桌上剩下的牙签（44或40根）拿起来，重复一遍第2、3、4步。即：随机分两堆—>从右堆拿1根夹着—>分别数两堆4的余数—>把所有余数组合起来。这次，你手上夹着的总数必定是4或者8。

把这新凑的一小堆（4或8根）也放到旁边，收拢桌上剩下的。

“三变”：把桌上再次剩下的牙签拿起来，再重复一遍第2、3、4步。这次手上夹着的总数也必定是4或者8。

揭晓最终密码！

经过了这三轮复杂的操作（称为“三变”），桌上最后还剩下一些牙签。

数一数它们有多少根。

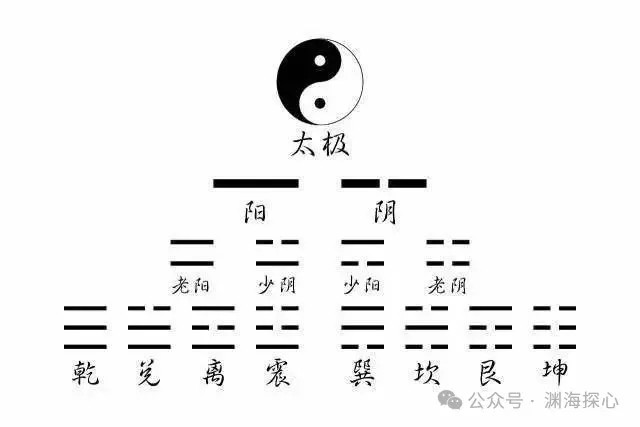
这个数量必定是36、32、28、或24。

最后一步，把这个数字除以4！

36÷4 = 9 (称为“老阳”，是变爻)

32÷4 = 8 (称为“少阴”，是静爻)

28÷4 = 7 (称为“少阳”，是静爻)

24÷4 = 6 (称为“老阴”，是变爻)

恭喜！已经通过“大衍术”得出了第一爻的数字（6、7、8、9之一）。然后，把全部49根牙签收拢，从头到尾再把这个极其复杂的过程重复五次，就能得到剩下的五爻，从而组成一个完整的卦象。

我们这里主要解释下，

为什么第一次“一变”总是剩5或9？

我们有49根。49 = 48 + 1。

你先拿走1根（夹在小指），剩下48根。

你把48根分成左右两堆（左+右=48）。

重点来了：48是4的倍数。

所以，左堆除以4的余数，加上右堆除以4的余数，其和也必然是4的倍数（只可能是4或8，不可能是0因为两堆至少都有1根）。

但实际操作是，你从右堆先拿了1根，所以实际数的是(左-1)。那么 左+ (右-1) = 47。再来数余数。左mod 4 + (右-1) mod 4。

mod是取余符号。

例如，如果左是9，右是40。

那么9 mod 4 = 1。(40-1) mod 4 = 39 mod 4 = 3。

收集到的余数就是1 (挂一) + 1 (左余数) + 3 (右余数) = 5。

而经过严谨的数学穷举可以证明，无论你怎么分，1 + (左mod 4) + ((右-1) mod 4)的结果，只有5和9两种可能。

第二次二变和第三次三变，

都依此类推。

说到这里，我们再来回头说，

大衍求一术（中国剩余定理）和大衍术（卜蓍法），

具体有什么联系。

这两种看似完全不同领域的术法，

共同展现了古代中国数学思想中一个极其深刻的智慧：

通过“余数”来掌控“本体”。

而且它们都属于构造性的思维典范。

因为，两者都不是通过暴力穷举去寻找答案，

而是通过巧妙的步骤一步步地构造出最终结果。

《易经》通过三轮归奇（收集余数），

将这些中间部件（每变拿走的蓍草数）从总数中剔除，

剩下的部分就是最终的结果。

中国剩余定理通过构造几个“基础解”，

然后将它们线性叠加，最终构造出总解。

不仅如此，它们都体现了“化繁为简”的降维思想。

处理一个大数字本身是很复杂的，

但处理它关于某个小数字的余数，就简单多了。

《易经》不去直接处理49这么个数，

而是通过反复求它关于4的余数，来推动整个过程。

中国剩余定理不去直接处理未知的巨大数字x，

而是分别研究它在3、5、7等小数世界里的“投影”（余数），

再把这些投影拼回原像。

所以，它俩都从模运算出发，

一个流向了哲学和宇宙论的田野，

一个流向了纯粹数学和应用科学的江河。

这也是为什么古代数学家秦九韶一直到我这边，

都在说，内算和外算密不可分，

因为它们本质的思想，

是直接相通的。